-10°

Существует много различных систем координат. Все они служат для определения положения точек на земной поверхности. Сюда относятся главным образом географические координаты, плоские прямоугольные и полярные координаты. Вообще координатами принято называть угловые и линейные величины, определяющие положение точек на какой-либо поверхности или в пространстве.

Географические координаты — это угловые величины — широта и долгота, определяющие положение точки на земном шаре. Географической широтой называется угол, образованный плоскостью экватора и отвесной линией в данной точке земной поверхности (рис. 25). Эта величина угла показывает, насколько та или иная точка на земном шаре севернее или южнее экватора. Если точка

расположена в Северном полушарии, то ее географическая широта будет называться северной, а если в Южном полушарии — южной широтой. Широта точек, расположенных на экваторе, равна нулю (0°), а на полюсах (Северном и Южном) — 90°.

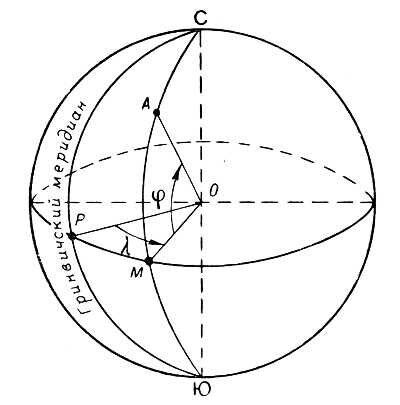
Рисунок 25.

Географической долготой также является угол, но образованный плоскостью меридиана, принятого за начальный (нулевой), и плоскостью меридиана, проходящего через данную точку.

Для однообразия определения долгот условились начальным меридианом считать меридиан, проходящий через астрономическую обсерваторию в Гринвиче (близ Лондона) и именовать его Гринвичским. Все точки, расположенные от него к востоку, будут иметь восточную долготу (до меридиана 180°), а к западу от начального — западную долготу.

На рисунке 25 показано, как определять положение точки А на земной поверхности, если известны ее географические координаты (широта — ф и долгота — к). Заметим, что разность долгот двух пунктов на Земле показывает не только их взаимное расположение по отношению к нулевому меридиану, но и разницу во времени в этих пунктах в один и тот же момент. Дело в том, что каждые 15° (24-я часть окружности) по долготе равны одному часу времени. Исходя из этого, можно по географической долготе определять разность во времени в этих двух точках.

Пример. Москва имеет долготу 37°37′ (восточную), а Хабаровск — 135°05′, то есть лежит восточнее 97°28′ Какое время имеют эти города в один и тот же момент?

Простые расчеты показывают, что если в Москве 13 часов, то в Хабаровске 19 часов 30 минут.

Как же определяют географические координаты по карте?

На рисунке 42 показано оформление рамки листа любой топографической карты. Как видно из рисунка, в углах этой карты подписываются долгота меридианов и широта параллелей, образующих рамку листа данной карты.

Со всех сторон рамка имеет шкалы, разбитые на минуты (и для широты и для долготы). Более того, каждая минута точками разделена на 6 равных участков, которые соответствуют 10 секундам долготы или широты. Таким образом, для того, чтобы определить широту какой-либо точки М на карте (рис. 42), надо через эту точку провести линию, параллельную нижней или верхней рамке карты, и прочитать справа или слева по шкале широты, соответствующие градусы, минуты, секунды. В нашем примере точка М имеет широту ф = 45°31′30″. Аналогично, проводя вертикаль через точку М параллельно боковому (ближнему к данной точке) меридиану границы данного листа карты, читаем долготу (восточную) I = 43°31′18″ . Нанесение на карту точки по заданным географическим координатам производится в обратной последовательности. Вначале находят на шкалах указанные географические координаты, а потом через них проводят параллельную и перпендикулярную линии. Пересечение их на карте покажет точку с заданными географическими координатами.

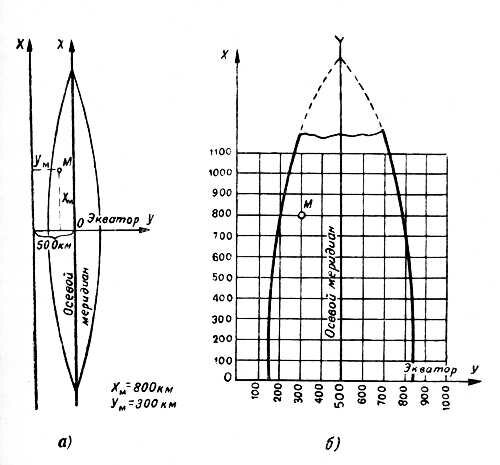
Рисунок 26.

Линии параллелей и меридианов, которые служат рамкой для данного листа карты, представляют собой кривые линии, хотя кривизна их в пределах одного листа практически и незаметна. Но в пределах каждой зоны Гаусса имеются две линии, которые изображаются на карте прямыми линиями,— это осевой меридиан зоны и экватор (рис. 26). Эти две линии приняты за оси плоских прямоугольных координат. Линию осевого меридиана считают осью абсцисс и обозначают х, линию экватора — осью ординат и обозначают у. За начало координат принимают точку пересечения осевого меридиана с экватором. Таким образом, в каждой зоне Гаусса имеется своя сетка плоских прямоугольных координат. Координаты х (абсциссы) отсчитываются к северу и югу от экватора, то есть от 0 (на экваторе) до 10 000 км (на полюсе). К северу от экватора координата у считается положительной, к югу — отрицательной. Координаты ху (ординаты) отсчитываются от осевого меридиана вправо (к востоку) и влево (к западу). Чтобы не иметь дела с отрицательными значениями для этих координат, условились значение ординаты у для осевого меридиана принимать равным 500 км. Тем самым ось х как бы переносится к западу на 500 км и все значения ординат в пределах данной зоны будут иметь всегда положительный знак. Кроме того, к значению ординаты у спереди всегда приписывается цифра, соответствующая номеру зоны Гаусса для того, чтобы избежать повторения координат, расположенных в разных зонах.

Для определения плоских прямоугольных координат точек в каждой зоне Гаусса на топографических картах наносится прямоугольная сетка координат (рис. 26), то есть проводятся линии, параллельные осевому меридиану и экватору.

Эти прямые линии, естественно, не будут совпадать с линиями, изображающими меридианы и параллели (за исключением осевого меридиана и экватора, параллельно которым они проводятся). Эту сетку координат называют километровой, так как ее линии проводятся через километр (для масштабов 1 : 10 000, 1 : 25 000, 1 : 50 000).

На каждом листе карты вдоль внутренней рамки даются значения координат километровой сетки от осевого меридиана данной зоны и от экватора. Как видно из рисунка 42, значения полных координат подписываются только у крайних (верхней и нижней) линии сетки координат. У всех же промежуточных линий подписываются сокращенные обозначения, то есть только последние две цифры (десятки и единицы километров). Например, нижняя линия километровой сетки (рис. 42) имеет обозначение 5042, а следующая над ней линия сетки обозначена только цифрой 43 км, а не 5043. Цифры километровой сетки под южной и над северной рамкой листа карты обозначают ординаты (у) этих линий. Крайние линии также обозначены полными координатами. Но в отличие от горизонтальных линий, первая цифра у ординат обозначает номер зоны. Например, ордината у = 8384 км. Это значит, что лист данной карты расположен в восьмой шестиградусной зоне Гаусса, то есть ограниченной 42 и 48° меридианами восточной долготы, а точки, лежащие на линии у = 384, расположены   слева   от   осевого   меридиана   на   расстоянии

500 — 384 – 116 км.

С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить координаты любой точки на карте (с точностью до километра). Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М (рис. 42), и прочитать цифры, обозначающие данный квадрат. Сначала обычно называется (записывается) значение координаты х = 5044, а затем у = 8384.

Для указания какого-либо объекта на карте обычно говорят так: точка М находится в квадрате 50 448 384, то есть называют координаты ее подряд, не разделяя их, но чаще дают указания сокращенно, называют только две последующие цифры из прямоугольных координат данной точки — квадрат 4484. Называя этот квадрат на карте, мы указываем координаты левого нижнего его угла, то есть юго-западного угла квадрата, в котором расположена точка М. Если необходимо указать более точное положение точки внутри этого квадрата, то дополнительно определяют ее расстояние от граничных линий этого квадрата. Используя  масштаб,  переводят  эти расстояния  в метры и приписывают их к цифрам обозначенного квадрата. Например,    точка    М   имеет    следующие    координаты: х == 44 500 м, а г/ = 84 500 м. Это и будут сокращенные координаты для точки М, а полные координаты для нее запишутся так: х = 5 044500 м, у — 384 500 м.

Нанесение точек на карту по известным плоским прямоугольным координатам производится в обратной последовательности. Сначала отбрасываются три последние цифры в координатах и находятся линии километровой сетки, то есть квадрат, в котором расположена точка. Затем, с помощью линейки, масштаба и циркуля, наносятся точные координаты данной точки в этом квадрате.

На некоторых топографических картах можно встретить две сетки плоских прямоугольных координат, одна нанесена полностью так, как это было показано на рисунке 42, а вторая обозначена только за рамкой данной карты. В чем тут дело? Мы уже ранее установили, что вертикальные километровые линии параллельны осевому меридиану своей зоны (рис. 26), а осевые меридианы соседних зон между собой не параллельны. Следовательно, при стыковке километровых сеток двух соседних зон линии одной из них располагаются под углом к линиям другой. Вследствие этого на стыке двух зон могут возникнуть затруднения в определении координат, так как они будут относиться к разным осям координат. Чтобы устранить это неудобство, в каждой шестиградусной зоне все листы карт, расположенные в пределах 2° к востоку и 2° к западу от границы зоны имеют помимо своей координатной сетки еще и дополнительную, являющуюся продолжением координатной сетки соседней зоны. И для того чтобы не затемнять второй сеткой данные листы карты, ее обозначают лишь цифрами на внешней рамке листа. Цифры эти являются продолжением нумерации линий координатной сетки смежной зоны. Итак, мы рассмотрели, как определяются географические координаты и плоские прямоугольные координаты отдельных точек на топографической карте.

С появлением радиолокации и радиопеленгации появилась необходимость в определении на карте и на местности положения отдельных точек с помощью угла относительно какого-либо направления и расстояния до них от какой-то выбранной точки, которую называют полюсом.

Если мы возьмем вместо двух взаимно перпендикулярных осей х и у в системе плоских прямоугольных координат только одну ось х и начальную точку на ней 0 (полюс) и от нее определим угол а (альфа) (рис. 27), который называется углом положения, а также расстояние Д (от полюса до точки), то эти две величины носят наименование «полярные координаты». В полярных координатах ось х называется полярной осью, а угол положения отдельной точки может иметь три обозначения и соответственно три наименования: дирекционный угол а, истинный азимут А и магнитный азимут Ам.

Такое большое количество углов положения и их разное наименование объясняются тем, что именно мы примем за полярную ось в системе полярных координат, от какого направления мы будем   замерять угол положения.

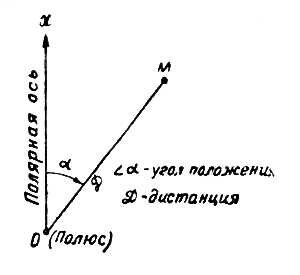
Рисунок 27.

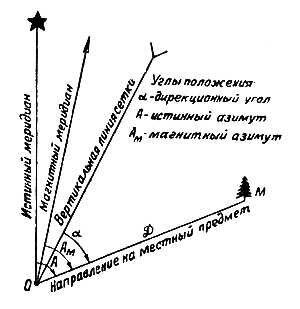
Рисунок 28.

Если мы за полярную ось возьмем направление вертикальной линии координатной сетки (рис. 28), то тогда этот угол будет называться дирекционным углом и обозначаться а; если за полярную ось мы возьмем направление истинного меридиана (а он имеется на карте), то этот угол будет называться истинным азимутом и обозначаться А. II, наконец, если мы возьмем за полярную ось магнитный меридиан (направление магнитной стрелки компаса), то этот угол положения носит название магнитный азимут и будет обозначаться Ам .

Во всех этих случаях угол положения изменяется от О до 360° и обязательно замеряется по ходу часовой стрелки.

Если установить соотношение полярных осей между собой, то тогда будет определено и соотношение между дирекционным углом а, истинным и магнитным азимутами А и Ам.

Выше мы уже установили, что вертикальные линии прямоугольной сетки координат составляют некоторый угол с меридианами, то есть боковыми сторонами рамки карты (рис. 29). Причина этого заключается в том, что все меридианы сходятся у полюсов, а вертикальные линии сетки остаются параллельными своему осевому меридиану зоны.

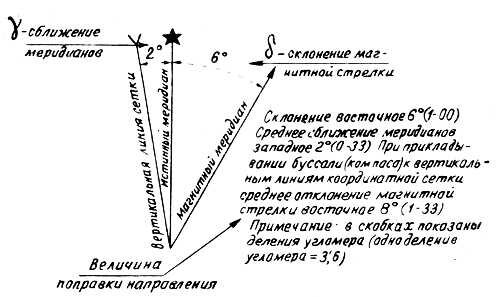
Рисунок 29.

Угол, составленный истинным меридианом в данной точке и вертикальной линией сетки, проходящей через эту же точку, называют сближением меридианов и обозначают греческой буквой γ(гамма).

Сближение меридианов бывает восточное (со знаком +), когда координатная сетка имеет наклон вправо относительно рамки карты, и западное (со знаком —), когда координатная сетка имеет наклон влево. Если угол сближения меридианов достигает 1° и более, его надо учитывать при переходе от дирекционного угла (а )к истинному азимуту (А). Величина его на краях зоны достигает 3°.

Истинный  меридиан  в  свою  очередь не  совпадает с магнитным (который показывает стрелка компаса). Этот угол между ними  называется   магнитным   склонением и обозначается греческой буквой σ(дельта). Магнитное склонение считается восточным (со знаком +), если северный конец магнитной стрелки компаса уклоняется к востоку от истинного меридиана, и западным (со знаком —) при уклонении к западу. Сложность с учетом магнитного склонения при переходе от дирекционного угла к магнитному азимуту заключается в том, что в силу магнитных свойств Земли оно в разных пунктах земной поверхности неодинаково. Более того, на одном и том же месте оно также не остается постоянным, а из года в год изменяется.

Таким образом, из сказанного видно, что вертикальные линии координатной сетки и магнитные меридианы образуют между собой угол, представляющий сумму сближения меридианов у и магнитного склонения (6). Этот угол называют углом отклонения магнитной стрелки, или поправкой направления, и обозначают заглавной буквой — П = Y + 6.

Поправка направления П отсчитывается от северного направления вертикальной линии координатной сетки и считается положительной (со знаком +), если северный конец магнитной стрелки отклоняется к востоку от этой линии, и отрицательной (со знаком — ) при западном отклонении магнитной стрелки. Данные о величине поправки направления (П) и ее слагающих величин: сближение меридианов (у), магнитное склонение (6), помещают в виде схемы под нижней рамкой листа карты с пояснениями (рис. 29). Эти данные необходимы для того, чтобы быстро переходить от дирекционных углов а, измеренных по карте, к соответствующим им магнитным азимутам (Ам) на местности. Для данной схемы соотношения между углом положения и поправкой будут выглядеть так:

Если же нам известен дирекционный угол и по нему надо определить магнитный азимут, то формула примет вид:

Все это справедливо только при восточном магнитном склонении ( + 6) и западном сближении меридианов (—у). Для других же схем поправка направления может быть равна не сумме этих углов, а разности или, более того, она сама может стать отрицательной. Тогда при переходе от дирекционного угла ( а) к магнитному азимуту в формуле (1) ее надо вычитать, а в формуле (2), наоборот, прибавлять.

Это обстоятельство заставляет каждого работающего с картой внимательно изучить схему расположения линии вертикальной сетки; истинного и магнитного меридианов и данные о величине поправки, помещаемые на каждой топографической карте.

Ошибки, допущенные в определении поправки направления (П) и тем более в ее знаке при определении данных по карте для движения по азимутам по местности, опасны тем, что при их величине в 5° и при движении на расстояние до 1 км отклонение в конце пути может составить около 100 м. Если это на открытой местности, то ориентир еще может быть обнаружен. Но на закрытой местности (в лесу) найти его уже почти невозможно.

Итак, мы рассмотрели вопросы, касающиеся методов и способов создания топографических карт (картографическая проекция Гаусса) и их возможных масштабов, разграфки и номенклатуры карт, а также вопросы, показывающие, как устроен каркас карт (географические меридианы и параллели, сетка плоских прямоугольных координат). Мы теперь умеем определять дирекционные углы, истинные и магнитные азимуты, поправку направления и осуществлять переход от одних углов к другим. Настало время заполнить каркас карты изображением местности и научиться читать ее, то есть изучить азбуку карты.